Tracking Down the Origin of Neutrino Mass
- Department of Theoretical Physics, CERN, Geneva, Switzerland
• Physics 16, 20
Collider experiments have set new direct limits on the existence of hypothetical heavy neutrinos, helping to constrain how ordinary neutrinos get their mass.
The discovery over 20 years ago that neutrinos can oscillate from one type to another came as a surprise to particle physicists, as these oscillations require that neutrinos have mass—contrary to the standard model of particle physics. While multiple neutrino experiments continue to constrain oscillation rates and mass values (see Viewpoint: Long-Baseline Neutrino Experiments March On), one fundamental question remains unanswered: How do neutrinos get their mass? Many theoretical models exist, but so far none of them have been experimentally confirmed. Now the CMS Collaboration at CERN in Switzerland has presented results on a search for a hypothetical heavy neutrino that could be tied to neutrino mass generation [1]. No signatures of this particle were found, placing new constraints on a popular model for the origin of neutrino mass, called the seesaw mechanism. These results pave a new way to probe the neutrino mass origin at particle colliders in the future.
There are clues that neutrino masses might be special. Neutrinos have no electric charge—making them distinct from other “matter” particles, such as electrons and quarks. Neutrinos are also unique in being observed with just one type of handedness (a property that emerges from the particle mass and spin). Other matter particles can be either left-handed or right-handed and obtain their mass via their interaction with the so-called Higgs field (see Focus: Nobel Prize—Why Particles Have Mass). The fact that neutrinos are observed to be only left-handed could suggest that the Higgs mechanism doesn’t apply to them.
There is another special feature of neutrinos: they are much lighter than all the other elementary particles. Experiments constrain neutrinos to be at least a million times lighter than electrons, the next lightest particles. This disparity suggests that something is “pushing” the neutrino mass toward small values. The seesaw mechanism includes such a push [2–7]. Just like on a playground, two players are involved in this metaphorical seesaw: an observed neutrino on one end and a hypothetical neutrino on the other (Fig. 1). The quantum states of these two particles are mixed—meaning that one particle can potentially oscillate into the other. This mixing leads to an inverse relation between the masses of the two players: the heavier the hypothetical particle, the lighter the observed neutrino.
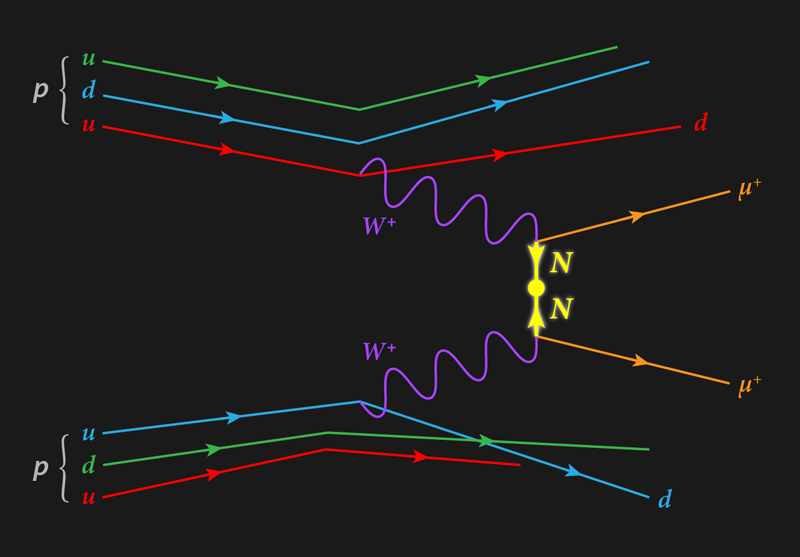
The heavy hypothetical neutrinos are “sterile” in that they do not participate in any of the known fundamental interactions. Another crucial feature of the seesaw mechanism is that neutrinos must be their own antiparticles—thus, evidence that neutrinos annihilate with themselves would provide support for this mechanism.
Researchers have for many years been searching for additional neutrinos. One probe involves observing neutrino oscillations and looking for signs of “missing” neutrinos. This scenario could occur, for example, if some of the electron neutrinos from a nuclear reactor transform into sterile neutrinos that can’t be detected. Some experiments have seen hints of sterile neutrinos (see Viewpoint: Neutrino Mystery Endures), but these possibly observed sterile neutrinos are much lighter than the predicted sterile neutrinos from the seesaw mechanism. At higher masses, global studies of neutrino data have uncovered no signs of missing neutrinos, allowing physicists to derive constraints on extra neutrinos that extend up to extremely high masses of 1015 GeV/c2.
A more direct search for additional neutrinos relies on producing them in high-energy experiments. The CMS Collaboration has hunted for signs of extra neutrinos in collision data from the Large Hadron Collider (LHC) at CERN. The team’s target signal was a violation of lepton number, which is a kind of “charge” related to electrons, muons, tauons, and neutrinos (Fig. 2). So far, physicists have only seen processes that conserve lepton number (see Viewpoint: The Hunt for No Neutrinos) [8], but dedicated searches at high energy have been rare [9]. In this new study, the CMS Collaboration looked for collisions between protons (lepton number of 0) that produced either a pair of muons (lepton number of +2) or a pair of antimuons (lepton number of −2). Observing such dimuon events would imply muon neutrinos annihilating with themselves via their coupling to sterile neutrinos.
The CMS team did not find evidence of lepton number violation in the muon data, which allowed the researchers to derive new bounds on the mixing of sterile neutrinos with muon neutrinos. These bounds improve over existing limits for sterile neutrino masses above 650 GeV/c2, and they represent the strongest bounds from colliders for sterile neutrino masses up to 25 TeV/c2. (It should be noted that oscillation experiments provide stronger bounds on sterile neutrinos, but these bounds do not include lepton number violation, and thus the relation to the seesaw mechanism is not straightforward [10].)
Putting these results into the context of the theoretical neutrino mass mechanism landscape, the CMS constraints on the mixing parameters are roughly 10 orders of magnitude weaker than the predicted values of these parameters in the simplest version of the seesaw mechanism. It is therefore unlikely that collider experiments can probe this simple version even in the future with more statistics and upgraded particle accelerators. Nevertheless, these results provide important constraints on popular variants of the seesaw mechanism, which generally feature larger mixings. In fact, these variants will continue to be a target of opportunity for future collider experiments, as well as for studies that combine searches for lepton number violation and searches for sterile neutrinos.
While neutrino oscillation experiments are nearing the determination of all the oscillation parameters, understanding the underlying mechanism of neutrino mass generation requires searches beyond oscillation experiments. These neutrino mass studies are progressing on multiple fronts, but so far they have provided only constraints—rather than a discovery of the origin of neutrino masses.
References
- A. Tumasyan et al. (CMS Collaboration), “Probing heavy Majorana neutrinos and the Weinberg operator through vector boson fusion processes in proton-proton collisions at s√� = 13 TeV,” Phys. Rev. Lett. 131, 011803 (2023).
- P. Minkowski, “μ→eγ𝜇→�𝛾 at a rate of one out of 109 muon decays?” Phys. Lett. B 67 (1977).
- P. Ramond, “The family group in grand unified theories,” (1979), arXiv:hep-ph/9809459.
- M. Gell-Mann et al., “Complex spinors and unified theories,” (1979), Conf. Proc. C 790927, arXiv:1306.4669.
- T. Yanagida, “Horizontal gauge symmetry and masses of neutrinos,” Conf. Proc. C 7902131 (1979) https://inspirehep.net/literature/143150.
- R. N. Mohapatra and G. Senjanović, “Neutrino mass and spontaneous parity nonconservation,” Phys. Rev. Lett. 44 (1980).
- J. Schechter and J. W. F. Valle, “Neutrino masses in SU(2) ⊗⊗ U(1) theories,” Phys. Rev. D 22 (1980).
- S. Abe et al. (KamLAND-Zen Collaboration), “First search for the Majorana nature of neutrinos in the inverted mass ordering region with KamLAND-Zen,” (2022), arXiv:2203.02139.
- B. Fuks et al., “Probing the Weinberg operator at colliders,” Phys. Rev. D 103 (2021).
- E. Fernandez-Martinez et al., “Global constraints on heavy neutrino mixing,” J. High Energy Phys. 2016 (2016).